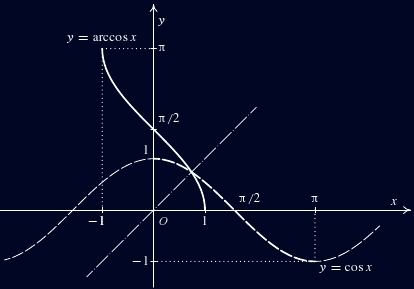
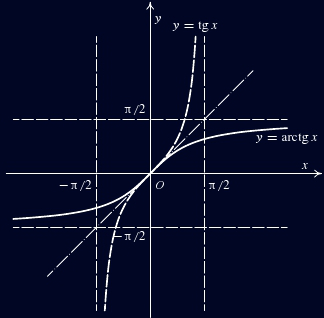
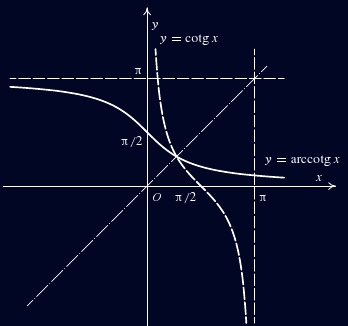
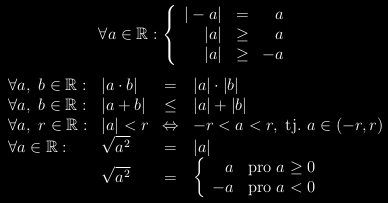Znáte ze střední školy
Definiční obor
Definiční obor
D algebraického výrazu jsou podmnožiny oborů proměnných, pro jejichž hodnoty má daný výraz smysl.
Pravidla pro stanovování definičního oboru algebraického výrazu:
- jmenovatel musí být různý od nuly,
- pod sudou odmocninou nesmí být záporné číslo.
Při úpravách lomených výrazů je nutné klást podmínky, že jmenovatel každého zlomku v původních výrazech i v upravených tvarech musí být různý od nuly.
Několik vzorečků
Při úpravách algebraických výrazů používáme například vzorce: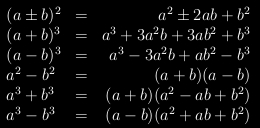
V oboru reálných čísel
R jsou kvadratický dvojčlen
a2+b2
a kvadratické trojčleny
a2-ab+b2, a2+ab+b2
nerozložitelné na součin lineárních dvojčlenů.
Počítání se zlomky
Mocniny a odmocniny
Odmocnina ze součtu se nerovná součtu odmocnin!!
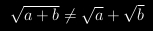
Absolutní hodnota
Každému reálnému číslu
a je přiřazeno právě jedno reálné číslo
|a| takto:
Některé vlastnosti absolutní hodnoty reálného čísla:
Základní funkce
exponenciální funkce
ex
| ax, a≥1
| ax, 0<a≤1
|
| D(f)=R | |
| H(f)=R+ |
|
logaritmické funkce
ln x |
logax
|
| D(f)=R+ |
| H(f)=R |
pravidla počítání s logaritmy |
logaxy=logax+logay
logaxn=nlogax |
logaa=1
loga1=0 |
|
mocninné funkce
xn, n:sudé, n>0 |
xn, n:liché, n>0 |
xn, n:sudé, n<0 |
xn, n:liché, n<0 |
| inverzní - odmocninné |
x1/n, n:sudé, n>0 |
x1/n, n:liché, n>0  |
|
goniometrické a cyklometrické funkce
sin x a arcsin x |
cos x a arccos x |
tg x a arctg x |
cotg x a arccotg x |
|
|